Transformer大致结构如下:
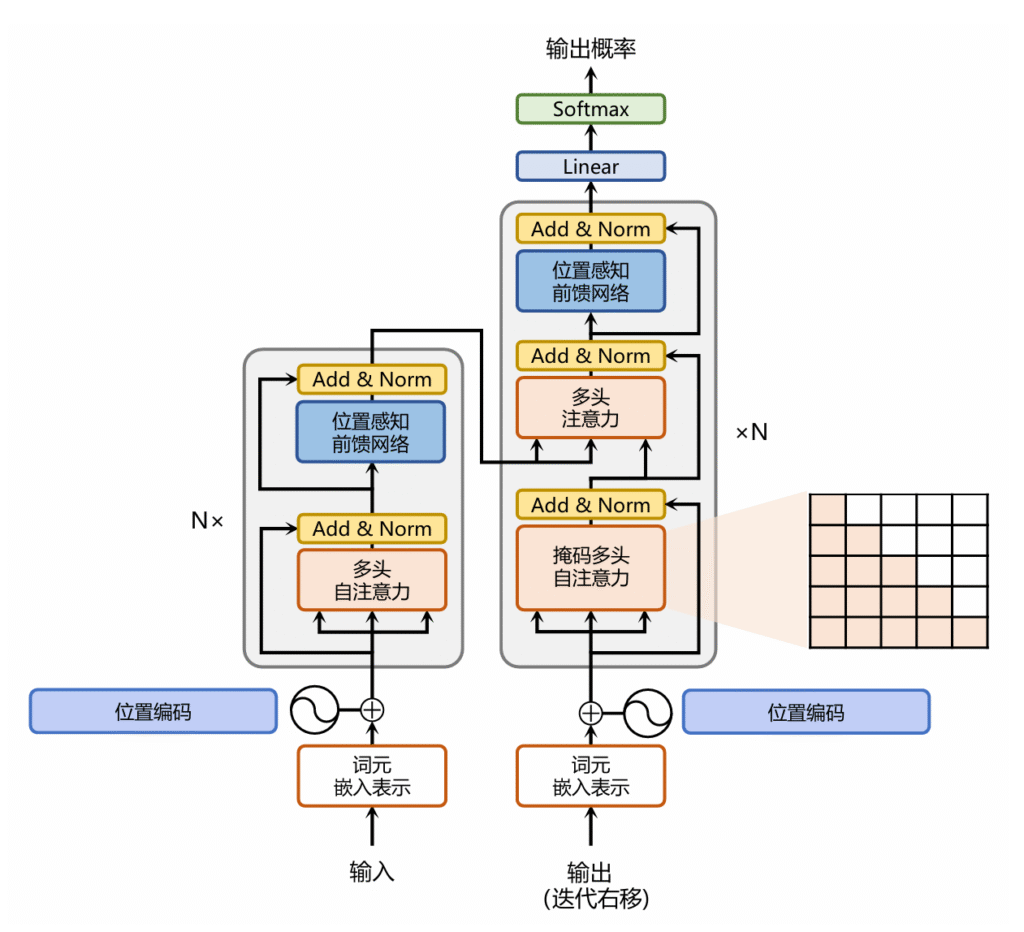
左侧灰框代表Encoder中的一层,右侧灰框是Decoder中的一层
灰框旁边的$N\times$代表多层组成一个完整的Encoder或Decoder
Add & Norm代表残差连接和归一化
Transformer的每个模块
位置编码
下面的公式中,2i和2i+1代表位置编码中对应的维度,d代表位置编码的总维度
$$PE(pos, 2i) = sin(\frac{pos}{10000^{\frac{2i}d}})$$
$$PE(pos, 2i+1) = cos(\frac{pos}{10000^{\frac{2i}d}})$$
简言之,当i为奇数的时候,使用cos计算i-1;当i为偶数时,使用sin计算i
class PositonEncoder(nn.Module):
def __init__(self, embedding_dim: int, max_len: int = 80, print_shape: bool = False):
super().__init__()
self.embedding_dim = embedding_dim
self.print_shape = print_shape
pe = torch.zeros(max_len, embedding_dim) # max_len * embedding_dim
if print_shape:
print("原始PE:", pe.shape)
for pos in range(max_len): # 每个token的索引
for i in range(0, embedding_dim, 2): # 单个token的位置编码的每个数
common = pow(10000, i / embedding_dim)
# 偶数
pe[pos][i] = math.sin(pos / common)
# 奇数
pe[pos][i + 1] = math.cos(pos / common)
pe.unsqueeze_(0) # 1 * max_len * embedding_dim
if print_shape:
print("PE unsqueeze(0):", pe.shape)
pe.requires_grad = False
self.register_buffer("pe", pe) # register_buffer用于记录不需要计算梯度但要跟随模型参数一起保存、加载或者移动(cuda)的变量
def forward(self, x: torch.Tensor):
# 让word embedding中的数字大一些,防止位置编码影响原有信息
x = x * math.sqrt(self.embedding_dim)
seq_len = x.size(1)
x += (self.get_buffer("pe")[:, :seq_len]) # 截取与seq_len一样长的位置编码,并加到x上
return x
## 以下是我自己加的一个decode函数,只是为了验证可以还原出原本的信息
def decode(self, x_with_pe: torch.Tensor):
seq_len = x_with_pe.size(1)
x_with_pe -= (self.get_buffer("pe")[:, :seq_len]) # 截取与seq_len一样长的位置编码,并加到x上
return x_with_pe / math.sqrt(self.embedding_dim)
# 是否开启详细输入
detail_print = True
# 指定Embedding的维度为D,实际会很多,这里为了学起来方便,就设置为4
D = 4
# 生成词的embedding,每个embedding的维度是D
fake_word_seq = torch.rand(1, 4, D)
pe = PositonEncoder(embedding_dim = D, print_shape=detail_print)
pe_result = pe(fake_word_seq)
if detail_print:
print("位置编码前:", fake_word_seq)
print("位置编码后:", pe_result)
decode_from_pe = pe.decode(pe_result)
print("还原出:", decode_from_pe)原始PE: torch.Size([80, 4])
PE unsqueeze(0): torch.Size([1, 80, 4])
位置编码前: tensor([[[0.9288, 0.9705, 0.9239, 0.3464],
[0.4873, 0.9059, 0.0731, 0.8387],
[0.6273, 0.6911, 0.3095, 0.2830],
[0.0837, 0.7790, 0.6491, 0.8472]]])
位置编码后: tensor([[[1.8575, 2.9410, 1.8477, 1.6928],
[1.8160, 2.3522, 0.1562, 2.6774],
[2.1639, 0.9661, 0.6390, 1.5658],
[0.3085, 0.5680, 1.3282, 2.6940]]])
还原出: tensor([[[0.9288, 0.9705, 0.9239, 0.3464],
[0.4873, 0.9059, 0.0731, 0.8387],
[0.6273, 0.6911, 0.3095, 0.2830],
[0.0837, 0.7790, 0.6491, 0.8472]]])多头注意力
将上述位置编码的输出记为X,则:$Q=XW^Q$、$K=XW^K$、$V=XW^V$
基于QKV计算Attention,记为Z,则:
$$Z=Attention(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d}})V$$
其中${QK^T}$被称为匹配分数,$\sqrt{d}$为缩放因子,在后续代码实现中设定$d=取整(词嵌入维度/头数)$,设置缩放因子是为了预防过大的${QK^T}$在Softmax中导致梯度爆炸和收敛慢的问题
头数可以理解为设置多组的$W^Q$、$W^K$、$W^V$,让不同的头有不同的侧重,得到不同的QKV,再分别求出不同的Z,记为$Z_i$
$$Z_i=Attention(Q_i,K_i,V_i)=Softmax(\frac{Q_i{K_i^T}}{\sqrt{d}})V_i$$
将每个头的Z连接,并经过一个线性变换($W^O$)得到最终的Z:
$$Z=Concat(Z_1,Z_2……Z_N)W^O$$
class MultiHeadAttention(nn.Module):
print_shape = detail_print
# 头的个数,embedding维度,dropout防止过拟合
def __init__(self, heads: int, embedding_dim: int, dropout: float = 0.1, print_shape: bool = False):
super().__init__()
self.print_shape = print_shape
self.embedding_dim = embedding_dim
self.d_k = embedding_dim // heads
self.sqrt_d = math.sqrt(self.d_k)
self.h = heads
self.w_q = nn.Linear(embedding_dim, embedding_dim)
self.w_k = nn.Linear(embedding_dim, embedding_dim)
self.w_v = nn.Linear(embedding_dim, embedding_dim)
self.dropout = nn.Dropout(dropout)
self.w_o = nn.Linear(embedding_dim, embedding_dim)
# 计算attention的函数
def attention(Q: torch.Tensor, K: torch.Tensor, V: torch.Tensor, sqrt_d: int, mask: torch.Tensor=None, dropout: float=None) -> torch.Tensor:
K_t = K.transpose(-2, -1) # k的倒数两个维度转置
scores = torch.matmul(Q, K_t) / sqrt_d # 匹配分数 / 缩放因子
# 有些分数不应当被计算,比如计算<PAD>(填充token),这种计算是没有意义的,所以要mask掉
if mask is not None:
if MultiHeadAttention.print_shape:
print("mask原始:", mask.shape)
mask.unsqueeze_(1)
if MultiHeadAttention.print_shape:
print("mask unsqueeze(1)", mask.shape)
# 如果mask对应位置为0,则使用一个很小很小的数字填充,使之经过Softmax之后几乎为0,避免影响后续计算
scores.masked_fill_(mask == 0, -1e9)
# 计算最后一个维度上的Softmax
scores = F.softmax(scores, dim=-1)
if dropout is not None:
scores = dropout(scores)
# 匹配分数 乘 V
return torch.matmul(scores, V)
def forward(self, q: torch.Tensor, k: torch.Tensor, v: torch.Tensor, mask=None):
batch_size = q.size(0)
# 我们就不设置多个w了,直接将线性计算的结果划分为多个head的结果,充分发挥并行计算的能力
Q: torch.Tensor = self.w_q(q)
Q = Q.view(batch_size, -1, self.h, self.d_k) # -1是指剩余的维度让计算机来计算
K: torch.Tensor = self.w_k(k).view(batch_size, -1, self.h, self.d_k)
V: torch.Tensor = self.w_v(v).view(batch_size, -1, self.h, self.d_k)
Q.transpose_(1, 2)
K.transpose_(1, 2)
V.transpose_(1, 2)
attention_result: torch.Tensor = MultiHeadAttention.attention(Q, K, V, self.sqrt_d, mask, self.dropout)
attention_result.transpose_(1, 2)
# contiguous是确保tensor在内存上是连续的,因为view只能在内存连续的tensor上操作
concat = attention_result.contiguous().view(batch_size, -1, self.embedding_dim)
return self.w_o(concat)
# 头的个数
H = 2
mha = MultiHeadAttention(H, D, print_shape=detail_print)
x_with_attention = mha(pe_result, pe_result, pe_result)
if detail_print:
print("x+attention:", x_with_attention)x+attention: tensor([[[ 0.1426, -0.4929, -0.3599, 0.1146],
[ 0.2438, -0.3386, -0.4638, 0.1055],
[ 0.1620, -0.4340, -0.4151, 0.0875],
[ 0.2331, -0.3243, -0.4994, 0.0760]]], grad_fn=<ViewBackward0>)前馈层
前馈层(FFN,前馈神经网络)接受注意力的输出作为输入,记为x
$$FFN(x) = ReLU(xW_1+b_1)W_2+b_2$$
实验表明增大前馈层的参数能提高结果质量,所以前馈层的维度一般比注意力要大
class FeedForward(nn.Module):
def __init__(self, embedding_dim, w_1_output_dim = 2048, dropout = 0.1):
super().__init__()
# w_1_output_dim 是xW_1+b_1的维度
self.w_1 = nn.Linear(embedding_dim, w_1_output_dim)
self.dropout = nn.Dropout(dropout)
self.w_2 = nn.Linear(w_1_output_dim, embedding_dim)
def forward(self, x):
w_1_output = self.w_1(x)
relu = F.relu(w_1_output)
relu = self.dropout(relu)
w_2_output = self.w_2(w_1_output)
return w_2_output
ffn = FeedForward(D)
ffn_result = ffn(x_with_attention)
if detail_print:
print("x+attention+ffn:", ffn_result)x+attention+ffn: tensor([[[-0.3077, -0.0482, -0.2723, 0.0226],
[-0.3204, -0.0588, -0.3143, 0.0235],
[-0.3227, -0.0638, -0.2851, 0.0350],
[-0.3355, -0.0763, -0.3167, 0.0379]]], grad_fn=<ViewBackward0>)残差连接和归一化
由于Transformer结构比较复杂,所以引入残差链接和层归一化技术来提升训练稳定性
残差链接是指将x直接加到output上(下面公式中的$l$代表第$l$层)
$$x^{l+1}=f(x^l)+x^l$$
同时为了保证每一层的输入和输出稳定在一个合理的范围中,引入了层归一化技术
$$LN(x)=\alpha·\frac{x-\mu}{\sigma}+b$$
其中$\mu$和$\sigma$分别表示均值和方差,用于将数据平移缩放到均值为0、方差为1的标准分布上;$\alpha$和$b$是要训练的两个参数
## 归一化
class Norm(nn.Module):
def __init__(self, embedding_dim, eps = 1e-6):
super().__init__()
self.size = embedding_dim
self.alpha = nn.Parameter(torch.ones(self.size))
self.bias = nn.Parameter(torch.zeros(self.size))
self.eps = eps
def forward(self, x: torch.Tensor):
mu = x.mean(dim=-1, keepdim=True)
sigma = x.std(dim=-1, keepdim=True)
norm = self.alpha * (x - mu) / sigma + self.bias
return norm
norm = Norm(D)
norm_result = norm(ffn_result)
if detail_print:
print("x+attention+norm:", norm_result)x+attention+norm: tensor([[[-0.9575, 0.6321, -0.7403, 1.0657],
[-0.8676, 0.6166, -0.8325, 1.0835],
[-0.9474, 0.5523, -0.7296, 1.1247],
[-0.8879, 0.5256, -0.7857, 1.1480]]], grad_fn=<AddBackward0>)Encoder和Decoder
Encoder
可以参考最上面的图,先实现一层EncoderLayer,再将多层EncoderLayer拼接成Encoder
class EncoderLayer(nn.Module):
def __init__(self, embedding_dim: int, heads: int, dropout = 0.1):
super().__init__()
self.attention = MultiHeadAttention(heads, embedding_dim, dropout)
self.feedforward = FeedForward(embedding_dim, embedding_dim * 256, dropout)
self.norm_1 = Norm(embedding_dim)
self.norm_2 = Norm(embedding_dim)
self.dropout_1 = nn.Dropout(dropout)
self.dropout_2 = nn.Dropout(dropout)
def forward(self, x, mask=None):
attention_output = self.attention(x, x, x, mask)
attention_output = self.dropout_1(attention_output)
x = attention_output + x # 残差连接
x = self.norm_1(x)
ffn_output = self.feedforward(x)
ffn_output = self.dropout_2(ffn_output)
x = ffn_output + x # 残差连接
x = self.norm_2(x)
return x在此基础上,就可以将embedding和位置编码融合进来,构建完整的Encoder了
class Encoder(nn.Module):
# 词表中词的数量,嵌入维度,几层EncoderLayer,头数,dropout
def __init__(self, vocab_size, embedding_dim, N, heads, dropout = 0.1, max_len = 80):
super().__init__()
self.N = N
self.embed = nn.Embedding(vocab_size)
self.pe = PositonEncoder(embedding_dim, max_len)
self.layers = [EncoderLayer(embedding_dim, heads, dropout) for _ in range(N)]
self.norm = Norm(embedding_dim)
def forward(self, src, mask):
x = self.embed(src)
x = self.pe(x)
for i in range(self.N):
x = self.layers[i](x, mask)
return self.norm(x)Decoder
同理,先实现DecoderLayer,再实现Decoder
class DecoderLayer(nn.Module):
def __init__(self, embedding_dim, heads, dropout = 0.1):
super().__init__()
self.norm_1 = Norm(embedding_dim)
self.norm_2 = Norm(embedding_dim)
self.norm_3 = Norm(embedding_dim)
self.attention_1 = MultiHeadAttention(heads, embedding_dim, dropout)
self.attention_2 = MultiHeadAttention(heads, embedding_dim, dropout)
self.feedforward = FeedForward(embedding_dim, embedding_dim * 256, dropout)
self.dropout_1 = nn.Dropout(dropout)
self.dropout_2 = nn.Dropout(dropout)
self.dropout_3 = nn.Dropout(dropout)
# encoder_outputs就是图中连接encoder和decoder的箭头
def forward(self, x, encoder_outputs, src_mask, target_mask):
# 生成下一次attention的q(查询)
attention_output = self.attention_1(x, x, x, target_mask)
attention_output = self.dropout_1(attention_output)
x = attention_output + x
x = self.norm_1(x)
# 使用上一次的q,去注意encoder输出的k和v,并且保证不会计算未生成的部分的数据
attention_output = self.attention_2(x, encoder_outputs, encoder_outputs, src_mask)
attention_output = self.dropout_2(attention_output)
x = attention_output + x
x = self.norm_2(x)
ffn_output = self.feedforward(x)
ffn_output = self.dropout_3(ffn_output)
x = ffn_output + x
x = self.norm_3(x)
return xclass Decoder(nn.Module):
def __init__(self, vocab_size, embedding_dim, N, heads, dropout = 0.1, max_len = 80):
super().__init__()
self.N = N
self.embed = nn.Embedding(vocab_size, embedding_dim)
self.pe = PositonEncoder(embedding_dim, max_len)
self.layers = [DecoderLayer(embedding_dim, heads, dropout) for _ in range(N)]
self.norm = Norm(embedding_dim)
def forward(self, target, encoder_outputs, src_mask, target_mask):
x = self.embed(target)
x = self.pe(x)
for i in range(self.N):
x = self.layers[i](x, encoder_outputs, src_mask, target_mask)
return self.norm(x)组装成Transformer吧!
class Transformer(nn.Module):
def __init__(self, src_vocab, target_vocab, embedding_dim, N, heads, dropout = 0.1,max_len = 80):
super().__init__()
self.encoder = Encoder(src_vocab, embedding_dim, N, heads, dropout, max_len)
self.decoder = Decoder(target_vocab, embedding_dim, N, heads, dropout, max_len)
self.out = nn.Linear(embedding_dim, target_vocab)
def forward(self, src, target, src_mask, target_mask):
encoder_outputs = self.encoder(src, src_mask)
decoder_output = self.decoder(target, encoder_outputs, src_mask, target_mask)
output = self.out(decoder_output)
return output